パラメトリック曲線
タエチャスク ナッチャノン 05241011
はじめに
本稿は東京大学コンピュータグラフィックス論の課題として日本語で記述するものである。 Glitchでの実装はコード周りの記述に不便な点があるため、個人のブログに記載することとした。 外部の方にも役立つ内容であることを期待する。
本稿では、コンピュータグラフィックスにおける基礎的な要素の一つ、パラメトリック曲線について説明する。
そもそも「パラメトリック」とは
よく見慣れている曲線の表現は という形で表されるものが多い。 例えば、 や などである。
それに対して、 が の値に(明示的に)依存せず、 と が両方ともパラメタ に依存するような曲線をパラメトリック曲線と呼ぶ。 例えば、円の方程式は次のように表される。
軸の描画
matplotlib と numpy を使ったことがあるならば、
np.linspace(0, 1, 100) のような関数を用い、頂点をサンプリングし、線分を描画することが見慣れているだろう。
WebGL も同様に、頂点のサンプリングを行って線分を繋いで描画することができる。
arange と linspace の具体的な実装を省略する。
const axes = [-1, 0, 1, 0, 0, -1, 0, 1];を定義する。
WebGL は基本的に Vertex Shader と Fragment Shader の二つのシェーダーを用いて描画を行う。Vertex Shader では、頂点の座標を受け取り、Fragment Shader では、その頂点の領域に色を付ける。
今回で扱うのは、渡した頂点をそのまま描画するだけのシェーダーである。
#version 300 es
in vec2 a_position;
void main() {
gl_Position = vec4(a_position, 0.0, 1.0);
}色も同様だが、uniform (自分の認識ではレンダーループの中で設定可能なもの) として受け取るようにする。
#version 300 es
precision mediump float;
out vec4 fragColor;
uniform vec4 uColor;
void main() {
fragColor = uColor;
}すると、シェーダーをコンパイルし、プログラムを作成する。(ヘルパー関数は省略)
const vertexShader = compileShader(gl, gl.VERTEX_SHADER, vertexShaderSource);
const fragmentShader = compileShader(
gl,
gl.FRAGMENT_SHADER,
fragmentShaderSource,
);
const program = createProgram(gl, vertexShader, fragmentShader);次に、頂点をバッファに格納する。
gl.useProgram(program);
const buffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(axes), gl.STATIC_DRAW);頂点の位置を指定するために、gl.getAttribLocation を用いて、シェーダーの中で a_position として定義した変数の位置を取得する。また、gl.getUniformLocation を用いて、uniform 変数の位置を取得する。
const posLocation = gl.getAttribLocation(program, "a_position");
const uColorLoc = gl.getUniformLocation(program, "uColor");次に、レンダーループの中で、
gl.useProgram(program);
gl.bindBuffer(gl.ARRAY_BUFFER, curveBuffer);
// 頂点の位置を指定
gl.enableVertexAttribArray(posLocation);
gl.vertexAttribPointer(posLocation, 2, gl.FLOAT, false, 0, 0);
// uniform 変数の位置を取得
gl.uniform4f(uColorLoc, 0.4, 0.0, 0.0, 1.0);
gl.drawArrays(gl.LINES, 0, 4); // 4つの頂点を描画以上より、座標軸を描画することができる。
簡単な曲線の描画
次に、円を描画する。円の頂点も同様に線分から形成されるため、allVertices にまとめる。
円の方程式から、 を から まで変化させることで、, の頂点を得ることができる。ここで とする。
const circle = linspace(0, 2 * Math.PI, 100).flatMap((theta) => [
0.5 * Math.cos(theta),
0.5 * Math.sin(theta),
]);
const allVertices = [...axes, ...circle];
// 以下は上記と同様
gl.useProgram(program);
const curveBuffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, curveBuffer);
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(allVertices), gl.STATIC_DRAW);レンダーループの中で、uniform 変数の位置を取得し、色を指定する。
gl.useProgram(curveProgram);
gl.bindBuffer(gl.ARRAY_BUFFER, curveBuffer);
gl.enableVertexAttribArray(curvePosLocation);
gl.vertexAttribPointer(curvePosLocation, 2, gl.FLOAT, false, 0, 0);
gl.uniform4f(uColorLoc_curve, 0.0, 0.4, 0.0, 1.0);
gl.drawArrays(gl.LINE_LOOP, 4, circle.length / 2);ということで、円を描画することができる。
ただし、画面をリサイズしたりすると、描画が崩れてしまうため、scaleMatrix を用いて、描画を行う。
#version 300 es
in vec2 a_position;
uniform mat4 u_scaleMatrix; // NEW
void main() {
gl_Position = u_scaleMatrix * vec4(a_position, 0.0, 1.0); // NEW
}最後に、u_scaleMatrix を uniform 変数として受け取り、gl_Position に掛け算を行う。
const aspectRatio = displayWidth / displayHeight;
const worldToGLScale = (PITCH * 2) / displayWidth;
const aspectScaleMatrix = glm.mat4.create();
glm.mat4.identity(aspectScaleMatrix);
glm.mat4.scale(aspectScaleMatrix, aspectScaleMatrix, [
worldToGLScale,
worldToGLScale * aspectRatio,
1,
]);
// 軸を描画するためには、-1 から 1 の範囲に収める必要があるため、identityMatrix を用意する。
const identityMatrix = glm.mat4.create();
glm.mat4.identity(identityMatrix);以下の scrollPassed は scroll の位置に応じて、描画を行うための関数である。この記事に特化した機能であるため、描画の本質には関係ない。
if (scrollPassed("show-axes")) {
gl.useProgram(curveProgram);
gl.bindBuffer(gl.ARRAY_BUFFER, curveBuffer);
gl.enableVertexAttribArray(curvePosLocation);
gl.vertexAttribPointer(curvePosLocation, 2, gl.FLOAT, false, 0, 0);
gl.uniformMatrix4fv(uScaleMatrixLoc, false, identity);
gl.uniform4f(uColorLoc_curve, 0.4, 0.0, 0.0, 1.0);
gl.drawArrays(gl.LINES, 0, 4);
}
if (scrollPassed("show-circle")) {
gl.useProgram(curveProgram);
gl.bindBuffer(gl.ARRAY_BUFFER, curveBuffer);
gl.enableVertexAttribArray(curvePosLocation);
gl.vertexAttribPointer(curvePosLocation, 2, gl.FLOAT, false, 0, 0);
gl.uniform4f(uColorLoc_curve, 0.0, 0.4, 0.0, 1.0);
gl.uniformMatrix4fv(uScaleMatrixLoc, false, aspectScaleMatrix);
gl.drawArrays(gl.LINE_LOOP, 4, circle.length / 2);
}ペンツール
本課題の工夫として、ペンツールを実装する。
まずは、頂点から実装してみよう。
- マウスの
EventListenerを登録する - 頂点を格納するための配列を用意する
- 頂点を描画する
ただし、これまでの描画は、頂点が事前に決まっており、STATIC_DRAW で描画していたが、今回は、頂点が動的に変化するため、どうすべきだろうか。
WebGL では、これまで使っていた gl.bufferData というバッファの管理を行う関数の他に、gl.bufferSubData という関数もある。
まずは、頂点を描画するためのシェーダーを用意する。
#version 300 es
in vec2 a_position;
uniform mat4 u_scaleMatrix;
void main() {
gl_Position = u_scaleMatrix * vec4(a_position, 0.0, 1.0);
gl_PointSize = 8.0;
}#version 300 es
precision mediump float;
out vec4 fragColor;
uniform vec4 u_color;
void main() {
float dist = length(gl_PointCoord - vec2(0.5, 0.5));
if (dist < 0.5) {
fragColor = u_color;
} else {
discard;
}
}次に、頂点を格納するための配列を用意する。
const vertices = useRef<glm.vec2[]>([]);React を使っているため、useRef を用いることにした。
pointProgram の作成段階を省略し、bufferData の部分を見てみる。
const MAX_POINTS = 1000;
const pointBuffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, pointBuffer);
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array(MAX_POINTS * 2),
gl.DYNAMIC_DRAW, // <- Use DYNAMIC_DRAW for dynamic data
);以上は MAX_POINTS を定義し、DYNAMIC_DRAW を指定することで、動的に変化するデータを格納することができる。
render ループの中で、gl.bufferSubData を用いて、頂点を格納する。
if (scrollPassed("show-points")) {
gl.useProgram(pointProgram);
gl.bindBuffer(gl.ARRAY_BUFFER, pointBuffer);
gl.enableVertexAttribArray(pointPosLocation);
gl.vertexAttribPointer(pointPosLocation, 2, gl.FLOAT, false, 0, 0);
gl.uniform4f(uColorLoc_point, 0.0, 0.0, 0.4, 1.0);
if (vertices.current.length > 0) {
gl.bufferSubData(
gl.ARRAY_BUFFER,
0,
new Float32Array(vertices.current.flatMap((v) => [v[0], v[1]])),
);
}
gl.uniformMatrix4fv(uScaleMatrixLoc_point, false, aspectScaleMatrix);
gl.drawArrays(gl.POINTS, 0, vertices.current.length);
}次に、mouse の EventListener を登録する。
function mouseDownHandler(e: MouseEvent) {
if (!canvasRef.current) return;
const [worldX, worldY] = screenToWorld(
e.clientX,
e.clientY,
canvasRef.current,
PITCH,
);
vertices.current.push(glm.vec2.fromValues(worldX, worldY));
}ポイントの移動
次に、頂点の十分に近くをクリックしたときに、頂点を選択できるようにする。
const mouseState = useRef<MouseState>({
x: 0,
y: 0,
isDown: false,
intersect: undefined,
picked: undefined,
});MouseState は、マウスの状態を管理するための型である。intersect は、頂点の 0.2 単位以内にマウスがあるときに、頂点を選択するためのものである。picked は、intersect の頂点を picked に格納するためのものである。それ以外 (picked でも、intersect でもない) には、マウスをクリックすると頂点が追加することになる。つまり、有限状態機械のようなものになる。
ポイントの選択
もっと複雑にすると、頂点をクリックしたとき洗濯中の状態にする。
const mouseState = useRef<MouseState>({
x: 0,
y: 0,
isDown: false,
intersect: undefined,
picked: undefined,
selected: undefined, // NEW
});さらに頂点を削除できるように keyboard の EventListener を登録する。
function keydownHandler(e: KeyboardEvent) {
if (e.key === "Escape") {
mouseState.current.selected = undefined;
}
if (e.key === "Delete" || e.key === "Backspace") {
if (mouseState.current.selected !== undefined) {
vertices.current.splice(mouseState.current.selected, 1);
mouseState.current.selected = undefined;
}
}
}マウスのスナップ
グリッドの近くに shift を押しながらマウスを動かすと、スナップするようにする。
type MouseState = {
x: number;
y: number;
isDown: boolean;
picked: number | undefined;
intersect: number | undefined;
selected: number | undefined;
shouldSnap: boolean; // NEW
};すでに world 座標に変換しているので、Math.round を用いて、スナップするようにする。
if (mouseState.current.shouldSnap) {
const x = Math.round(worldX);
const y = Math.round(worldY);
mouseState.current.x = x;
mouseState.current.y = y;
} else {
mouseState.current.x = worldX;
mouseState.current.y = worldY;
}ペンの状態機械
普通の直線ならば
selectedの点があるときに、別の点をクリックすると線が描画されるselectedの点があるときに、何もないところをクリックすると頂点が追加され、線が描画される
つないだ線は lines に格納する。
const lines = useRef<[number, number][]>([]);レンダーループの中で、lines を描画する。
if (lines.current.length > 0) {
const allLines = lines.current.flatMap((line) => {
const start = vertices.current[line[0]];
const end = vertices.current[line[1]];
return [start[0], start[1], end[0], end[1]];
});
gl.bufferSubData(gl.ARRAY_BUFFER, 0, new Float32Array(allLines));
gl.drawArrays(gl.LINES, 0, allLines.length / 2);
}コントロールポイントの追加
ついに、本課題(ベージェ曲線)の本題に入る。
- 線からの距離が threshold 以下のときに、線を選択するようにする。
- 点を追加すると、
verticesに格納し、対応するlinesに格納する。 - 削除の際に、
linesからも削除する。
大きなリファクタリング
class での実装
interface Vertex {
coords: [number, number];
isControlPoint: boolean;
relatedLines: Set<number>;
isNear(point: [number, number], threshold: number): boolean;
}
interface Line {
start: number;
end: number;
addVertexAt: (vertex: Vertex, index: number) => void;
isNear(point: [number, number], threshold: number): boolean;
nearestSegmentIndex: (
point: [number, number],
threshold: number,
vertexMap: VertexMap,
) => number;
}を作成し、Vertex と Line の intersection 確認を抽象化する。
Map の Wrapper
interface VertexMap {
items: Map<number, Vertex>;
nextId: number;
add(coords: [number, number], isControlPoint?: boolean): number;
delete(id: number, lineMap: LineMap): void;
get(id: number): Vertex | undefined;
set(id: number, vertex: Vertex): void;
entries(): IterableIterator<[number, Vertex]>;
size: number;
}
interface LineMap {
items: Map<number, Line>;
nextId: number;
add(start: number, end: number): number;
delete(id: number): void;
get(id: number): Line | undefined;
entries(): IterableIterator<[number, Line]>;
size: number;
}これらのインターフェースは item を追加・削除の際に、次の id を管理するためのものである。元々使っていた配列は削除すると全部ずれるため、Map を用いることにした。
n-次ベージェ曲線
次に、n-次ベージェ曲線を描画する。
class Line {
allVerticesRef: RefObject<VertexMap>;
vertices: number[];
cached: [number, number][] | undefined;
constructor(vertices: number[], allVerticesRef: RefObject<VertexMap>) {
this.vertices = vertices;
this.allVerticesRef = allVerticesRef;
}
getOrCompute() {
if (this.cached) {
return this.cached;
}
const computed = this.compute();
this.cached = computed;
return computed;
}
compute(): [number, number][] {
const v = this.allVerticesRef.current;
const vec = this.vertices.map((s) =>
// biome-ignore lint/style/noNonNullAssertion: <explanation>
glm.vec2.fromValues(...v.get(s)!.coords),
);
if (vec.length === 2) {
return vec.map((v) => [v[0], v[1]]) as [number, number][];
}
const T = 100;
const N = vec.length - 1;
const ts = linspace(0, 1, T);
const result = ts.map((t) => {
const res = glm.vec2.create();
for (let i = 0; i <= N; i++) {
const coefficient = comb(N, i) * t ** i * (1 - t) ** (N - i);
glm.vec2.scaleAndAdd(res, res, vec[i], coefficient);
}
return [res[0], res[1]];
});
return result as [number, number][];
}
invalidate() {
this.cached = undefined;
}
}べージェ曲線のための計算量が重いため、各線ごとにキャッシュを用意する。
compute が本題であるため、より詳細に説明する。
まずは、vertices を glm のベクトル化して、長さが 2 であれば、そのまま返せばいい。
次に、一定の間隔で をサンプリングし、ベージェ曲線の方程式を用いて、各点を計算する。
サンプリングは自作 linspace を用いることにした。
function linspace(start: number, end: number, num: number) {
return Array.from(
{ length: num },
(_, i) => start + (end - start) * (i / (num - 1)),
);
}もちろん、comb の実装でもキャッシュを用意する。
const combCache = new Map<[number, number], number>();
function comb(n: number, r: number): number {
const cached = combCache.get([n, r]);
if (cached) return cached;
if (r === 0) return 1;
if (r === 1) return n;
if (r > n / 2) return comb(n, n - r);
const res = Math.floor((n * comb(n - 1, r - 1)) / r);
combCache.set([n, r], res);
return res;
}次にサンプリングをした ts を map して、const coefficient = comb(N, i) * t ** i * (1 - t) ** (N - i) で計算された係数で重み付け和を取る。
描画の方は簡単に
for (const [idx, line] of lines.current.items) {
const segments = line.getOrCompute();
gl.bindBuffer(gl.ARRAY_BUFFER, curveBuffer);
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array(segments.flat()),
gl.STATIC_DRAW,
);
gl.enableVertexAttribArray(curvePosLocation);
gl.vertexAttribPointer(curvePosLocation, 2, gl.FLOAT, false, 0, 0);
gl.uniform4f(uColorLoc_curve, 0.0, 0.0, 0.0, 1.0);
gl.drawArrays(gl.LINE_STRIP, 0, segments.flat().length / 2);
}以上より、n-次ベージェ曲線のペンツールを実装することができた。
今後の改善点・工夫点
WebGL についてより詳しく知りたかったため、スクラッチから実装してみたが、理想的でないコードを書いてしまったかもしれない。
特に気になったのは render ループごとにバッファデータを動的に登録して描画することである。
また、UX 的にいうと、点を移動することができたり、できなくなったりことがあるので、それを踏まえて状態機械を見直すべきである。
最後に頂点を PITCH 倍ほど掛けて interpolation を計算認め、数値的安定性に関しては特に影響がみえなかった。より小さい World 座標で計算を行うとより複雑なサンプリング方法が必要である。
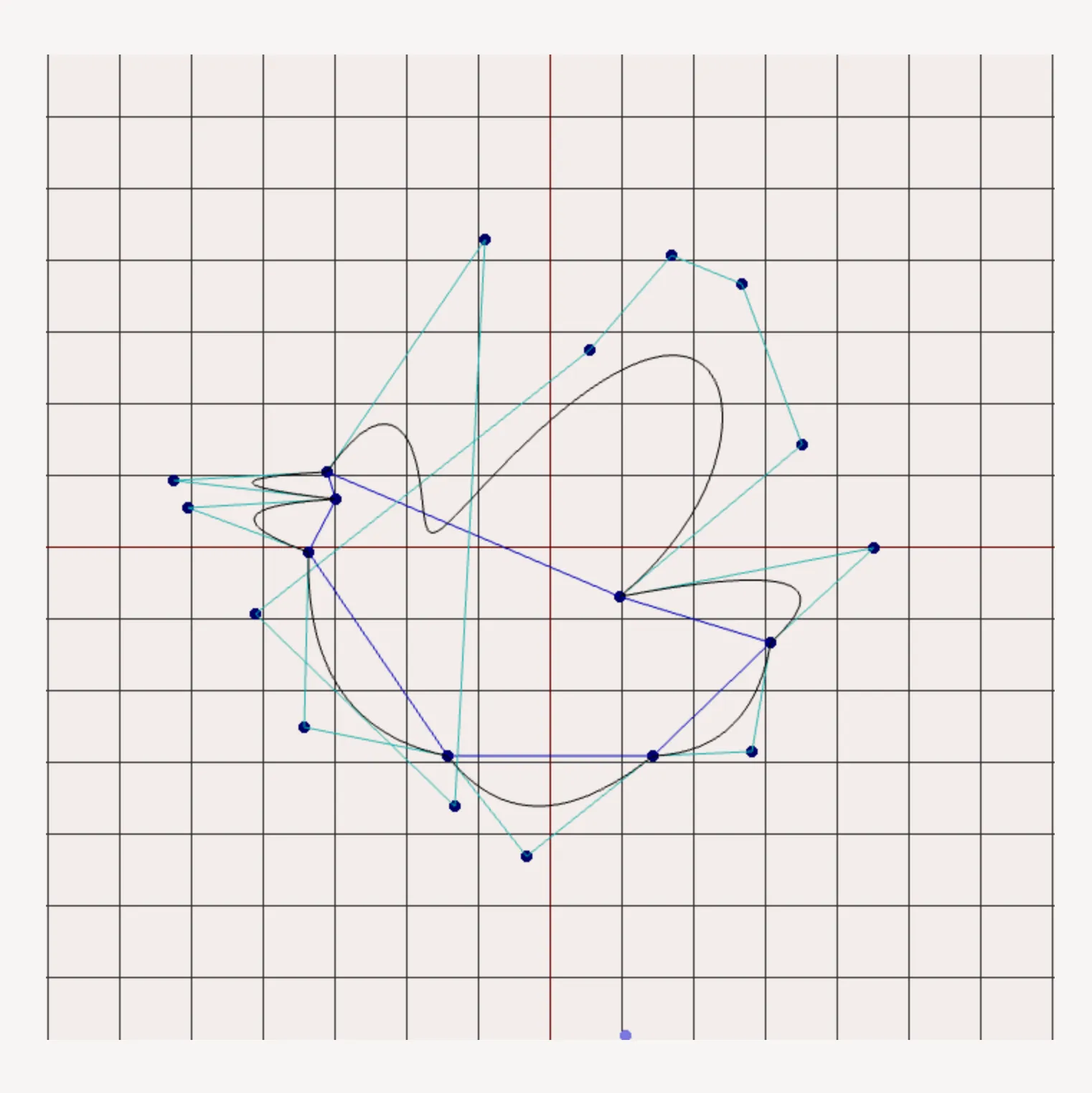
結果
こんな結果が得られた。